
Who: Nine early college students who are deeply but perhaps informally prepared
for mathematics research.
What: Eight weeks of mathematical research on combinatorial geometry of origami. More details.
When:
June 16th - Aug 10th, 2024 (8 weeks).
Where: Bryn Mawr College, alongside the participants in the
MathILy summer program. More details.
Why: Because students who are prepared for research should have
the opportunity to do it.

The application process: Consists of personal information, information about your mathematical
studies, a multi-question personal statement, and two recommendations (instructions will be sent to recommenders when you submit the aforementioned information), all of which must be received by April 2, 2024. More details.
Stipend: $4800, plus on-campus housing and meals while at
Bryn Mawr.
Research Description: In 2024 the MathILy-EST topic will be combinatorial geometry of origami, an area that mixes discrete mathematics, geometry, and analysis, under the direction of Dr. Thomas Hull.
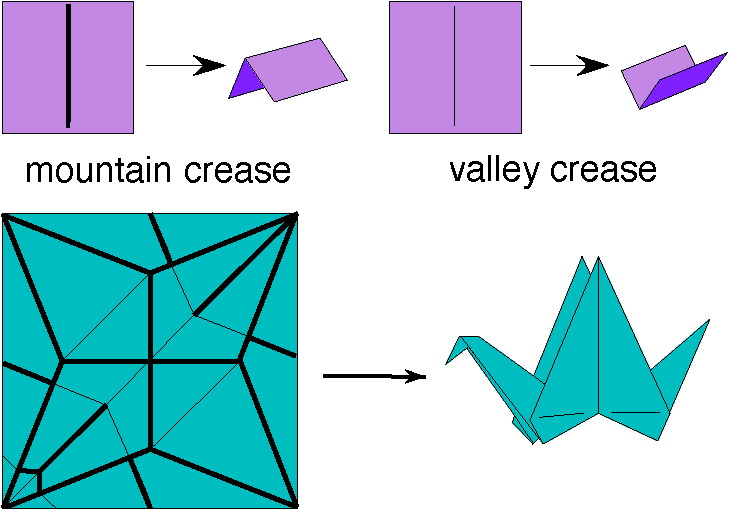
Crease and crease pattern examples
Origami is the art of folding paper, usually without making cuts, into interesting objects. Common to all mathematical studies of origami is the idea of a crease pattern, which is a planar graph \(C\) drawn on one's paper \(P\subset \mathbb{R}^2\) where the edges of \(C\), called creases, denote the folds made. Folded creases come in two types, mountains that fold away from your point of view and valleys that fold towards you. (Of course, flipping the paper over reverses all the mountain and valley creases.)
It turns out that understanding how origami works requires a mix of mathematical areas, and the problems we will undertake utilize aspects of geometry, combinatorics, and analysis. Many of these problems are motivated by applications, and this way of studying origami is relatively new in the world of mathematics.
A sample of the kinds of problems we will consider follows.
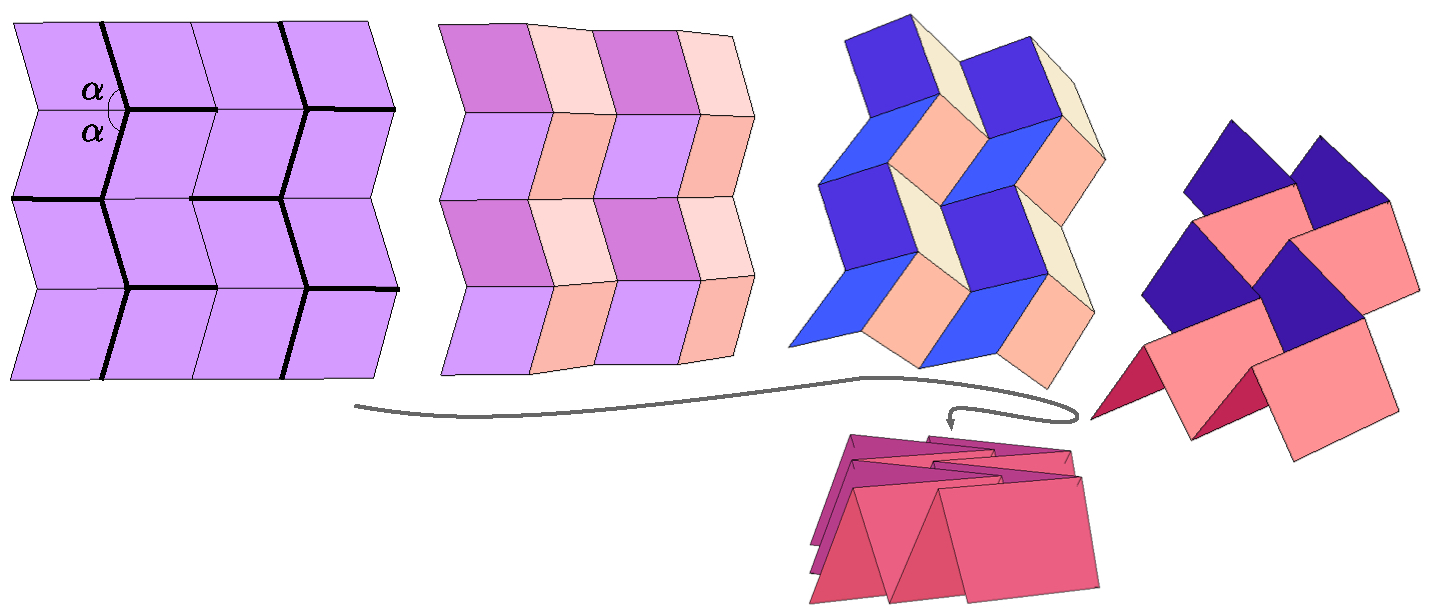
A rigid folding of the Miura-ori crease pattern
Origami has attracted the attention of physicists, engineers, and architects over the past 15 years. The intricate mechanics that rigid folding motions exhibit can be used in robotics and structure deployment. However, many open questions exist in the mathematics of such origami. A lot of progress on origami questions has been made in recent years, but many remain open, even for simple families of crease patterns.
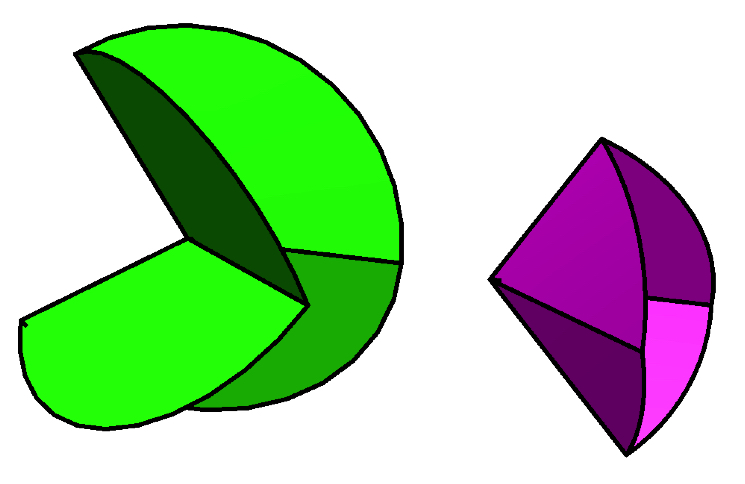
Vertices surrounded by more, or less, than 360 degrees of angle
Research Mentor: Dr. Thomas Hull is an Associate Professor of Applied Mathematics at Franklin and Marshall College in Lancaster, PA. He has been researching the mathematics of paper folding since 1990 and is considered one of the world experts on the topic. He has written two books on the math of folding: the research monograph Origametry and the educational book Project Origami on using paper folding as a vehicle to teach math.
Graduate Research Apprentice menTor at MathILy-EST (GReAT-EST): Natasha Ter-Saakov is a PhD student at Rutgers University specializing in combinatorics. As an undergraduate, Natasha studied mathematics (and computer science and education) at MIT. She participated in MathILy 2014 and 2015 and MathILy-EST 2019. When she is able to, Natasha enjoys fire spinning. At home, she can be found baking and even occasionally assembling IKEA furniture.
Goals and Expectations: During the summer, each of the participants will be expected to...

Blackboards, whiteboards, glass... we have it all.
Prerequisites: Applicants must be undergraduates in good standing. Preference will be given to first-year college students, with second-year and entering college students also considered for participation. NSF funding requires that participants must be US citizens or permanent residents.
Transitioning into Research: MathILy-EST participants will have little-to-no formal experience with mathematics research. To ease participants into the work they will be doing, the program will start with the research mentor providing an overview of the project that includes pointers to literature and concrete examples that are associated with questions to investigate. Participants will be assigned sets of readings that they then must present to one another, as well as hands-on explorations so that they can familiarize themselves with relevant examples and generate data as a start to working on open problems.
The weekly record of progress that participants are expected to keep will provide practice in writing formally and building in time for detailed feedback and revisions of writing. In addition, it will provide fodder for paper drafts once research has progressed to the point of publication, and regular presentations on research progress will provide participants with feedback on their research methods and presentation skills.

Professional development for MathILy-EST participants will include...
MathILy and MathILy-EST: The MathILy-EST REU will overlap with the MathILy summer program. The two programs share space---MathILy-EST participants will stay in the same dorms as MathILy students and instructors, and have work space in the same building as the MathILy classrooms---which will provide plenty of opportunities for social interactions, from casual mathematical conversations in the public areas of the dorm room to afternoon frisbee, board, and card games, to the annual Philadelphia trip.

After the Program: At the end of MathILy-EST, the research mentor will help participants put together plans for presenting their research at local and national conferences, and will check in regularly during the following semesters to make sure they're keeping to a reasonable timeline for preparing publications and conference presentations. In addition, MathILy-EST participants will be invited to the {MathILy, MathILy-Er, MathILy-EST} Yearly Gather at the Joint Mathematics Meetings, which will provide a chance to catch up with their fellow participants and to network with participants from other years and programs.
Why Bryn Mawr is an awesome
place to be in the summer:
The dorms are really nice, and have air conditioning. (So do the classrooms.)
You will have a single room.
The campus is beautiful...really beautiful. (video!) And very safe!
The food is excellent. (Still, if
you suddenly need pizza or snacks, there are pizza places and a
grocery store near campus.)
Laundry is free.
Campus is also right near a hospital, shopping center,
etc.
Philadelphia, which has tons to offer---including art and science and medicine and natural history museums, a zoo, shopping malls, a public market (both ingredients and prepared foods), the Italian
Market, the Declaration
of Independence (yes, the real
thing), the Liberty
Bell, and about a zillion other things---is a short train ride away.

Practical stuff: We'll give you all the details after you've applied and if you are admitted.
If after reading this whole page you still have questions, please do contact us at .
MathILy, MathILy-Er, and MathILy-EST are projects of the nonprofit organization Mathematical Staircase, Inc..